Metric distance network centrality

Calculate metric distance centralities from a geopandas GeoDataFrame.

import geopandas as gpd
import matplotlib.pyplot as plt
from cityseer.metrics import networks
from cityseer.tools import graphs, io

Prepare the network as shown in other examples. Working with the dual graph is recommended.

streets_gpd = gpd.read_file("data/madrid_streets/street_network.gpkg")
streets_gpd = streets_gpd.explode(reset_index=True)
G = io.nx_from_generic_geopandas(streets_gpd)
G_dual = graphs.nx_to_dual(G)

100%|██████████| 47155/47155 [00:03<00:00, 12037.10it/s]
INFO:cityseer.tools.graphs:Merging parallel edges within buffer of 1.
100%|██████████| 47129/47129 [00:00<00:00, 172336.30it/s]
INFO:cityseer.tools.graphs:Converting graph to dual.
INFO:cityseer.tools.graphs:Preparing dual nodes
100%|██████████| 47129/47129 [00:00<00:00, 82516.86it/s]
INFO:cityseer.tools.graphs:Preparing dual edges (splitting and welding geoms)
100%|██████████| 47129/47129 [00:24<00:00, 1911.70it/s]

Use network_structure_from_nx from the cityseer package’s io module to prepare the GeoDataFrames and NetworkStructure.

# prepare the data structures
nodes_gdf, _edges_gdf, network_structure = io.network_structure_from_nx(
    G_dual,
)

INFO:cityseer.tools.io:Preparing node and edge arrays from networkX graph.
100%|██████████| 47129/47129 [00:00<00:00, 112602.24it/s]
100%|██████████| 47129/47129 [00:08<00:00, 5319.38it/s]
INFO:cityseer.graph:Edge R-tree built successfully with 104026 items.

Use the node_centrality_shortest function from the cityseer package’s networks module to calculate shortest metric distance centralities. The function requires a NetworkStructure and nodes GeoDataFrame prepared with the network_structure_from_nx function in the previous step.

The function can calculate centralities for numerous distances at once via the distances parameter, which accepts a list of distances.

The function returns the nodes GeoDataFrame with the outputs of the centralities added as columns. The columns are named cc_{centrality}_{distance}. Standard geopandas functionality can be used to explore, visualise, or save the results. See the documentation for more information on the available centrality formulations.

distances = [500, 2000]
nodes_gdf = networks.node_centrality_shortest(
    network_structure=network_structure,
    nodes_gdf=nodes_gdf,
    distances=distances,
)
nodes_gdf.head()

INFO:cityseer.metrics.networks:Computing shortest path node centrality.
100%|██████████| 47129/47129 [00:06<00:00, 6999.56it/s] 
INFO:cityseer.config:Metrics computed for:
INFO:cityseer.config:Distance: 500m, Beta: 0.008, Walking Time: 6.25 minutes.
INFO:cityseer.config:Distance: 2000m, Beta: 0.002, Walking Time: 25.0 minutes.

	ns_node_idx	x	y	live	weight	primal_edge	primal_edge_node_a	primal_edge_node_b	primal_edge_idx	dual_node	...	cc_farness_500	cc_farness_2000	cc_harmonic_500	cc_harmonic_2000	cc_hillier_500	cc_hillier_2000	cc_betweenness_500	cc_betweenness_2000	cc_betweenness_beta_500	cc_betweenness_beta_2000
x454839.5-y4476885.3_x454855.9-y4476818.6_k0	0	454848.067543	4.476852e+06	True	1	LINESTRING (454855.9 4476818.6, 454849.1 44768...	x454855.9-y4476818.6	x454839.5-y4476885.3	0	POINT (454848.067543 4476852.042507)	...	7418.207031	163780.609375	0.199088	0.315512	0.121323	0.148589	0.0	0.0	0.000000	0.000000
x454833.6-y4476910.5_x454839.5-y4476885.3_k0	1	454836.577015	4.476898e+06	True	1	LINESTRING (454839.5 4476885.3, 454838 4476891...	x454839.5-y4476885.3	x454833.6-y4476910.5	0	POINT (454836.577015 4476897.9067)	...	10061.340820	162550.625000	0.294068	0.401464	0.143520	0.155527	127.0	1032.0	18.257139	174.897049
x454839.5-y4476885.3_x454877.1-y4476893.6_k0	2	454858.300000	4.476889e+06	True	1	LINESTRING (454839.5 4476885.3, 454877.1 44768...	x454839.5-y4476885.3	x454877.1-y4476893.6	0	POINT (454858.3 4476889.45)	...	8638.165039	167096.218750	0.313121	0.424865	0.133825	0.151296	99.0	753.0	18.619455	135.658371
x454823.1-y4476952.1_x454833.6-y4476910.5_k0	3	454828.362585	4.476931e+06	True	1	LINESTRING (454833.6 4476910.5, 454830.4 44769...	x454833.6-y4476910.5	x454823.1-y4476952.1	0	POINT (454828.362585 4476931.303206)	...	10452.841797	161801.937500	0.281164	0.389349	0.153068	0.160202	158.0	1308.0	17.099850	212.337875
x454758.1-y4476894.6_x454833.6-y4476910.5_k0	4	454795.845199	4.476903e+06	True	1	LINESTRING (454758.1 4476894.6, 454769.8 44768...	x454833.6-y4476910.5	x454758.1-y4476894.6	0	POINT (454795.845199 4476902.571916)	...	9720.205078	166860.078125	0.197214	0.307718	0.126026	0.151510	0.0	0.0	0.000000	0.000000

5 rows × 26 columns

nodes_gdf.columns

Index(['ns_node_idx', 'x', 'y', 'live', 'weight', 'primal_edge',
       'primal_edge_node_a', 'primal_edge_node_b', 'primal_edge_idx',
       'dual_node', 'cc_beta_500', 'cc_beta_2000', 'cc_cycles_500',
       'cc_cycles_2000', 'cc_density_500', 'cc_density_2000', 'cc_farness_500',
       'cc_farness_2000', 'cc_harmonic_500', 'cc_harmonic_2000',
       'cc_hillier_500', 'cc_hillier_2000', 'cc_betweenness_500',
       'cc_betweenness_2000', 'cc_betweenness_beta_500',
       'cc_betweenness_beta_2000'],
      dtype='object')

nodes_gdf["cc_betweenness_2000"].describe()

count     47129.000000
mean       9697.498047
std       14681.911133
min           0.000000
25%         701.000000
50%        3823.000000
75%       12501.000000
max      237420.000000
Name: cc_betweenness_2000, dtype: float64

fig, ax = plt.subplots(1, 1, figsize=(8, 6), facecolor="#1d1d1d")
nodes_gdf.plot(
    column="cc_harmonic_500",
    cmap="magma",
    legend=False,
    ax=ax,
)
ax.set_xlim(438500, 438500 + 3500)
ax.set_ylim(4472500, 4472500 + 3500)
ax.axis(False)

(np.float64(438500.0),
 np.float64(442000.0),
 np.float64(4472500.0),
 np.float64(4476000.0))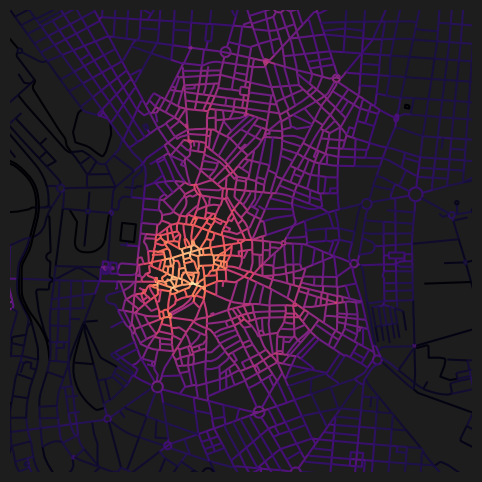

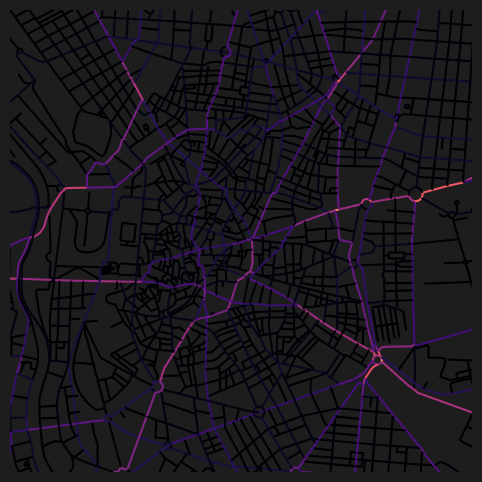
fig, ax = plt.subplots(1, 1, figsize=(8, 6), facecolor="#1d1d1d")
nodes_gdf.plot(
    column="cc_betweenness_2000",
    cmap="magma",
    legend=False,
    ax=ax,
)
ax.set_xlim(438500, 438500 + 3500)
ax.set_ylim(4472500, 4472500 + 3500)
ax.axis(False)

(np.float64(438500.0),
 np.float64(442000.0),
 np.float64(4472500.0),
 np.float64(4476000.0))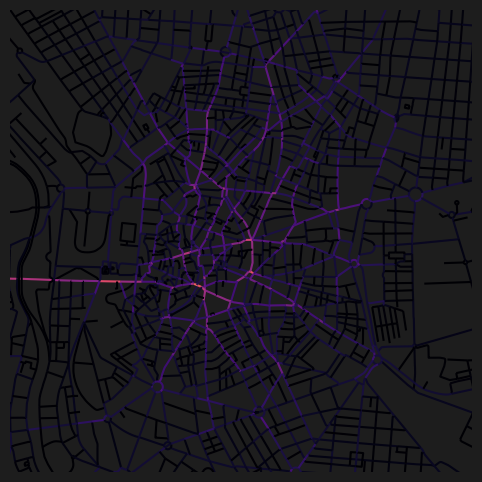

Alternatively, you can define the distance thresholds using a list of minutes instead.

nodes_gdf = networks.node_centrality_shortest(
    network_structure=network_structure,
    nodes_gdf=nodes_gdf,
    minutes=[15],
)

INFO:cityseer.metrics.networks:Computing shortest path node centrality.
100%|██████████| 47129/47129 [00:03<00:00, 15229.30it/s]
INFO:cityseer.config:Metrics computed for:
INFO:cityseer.config:Distance: 1200m, Beta: 0.00333, Walking Time: 15.0 minutes.

The function will map the minutes values into the equivalent distances, which are reported in the logged output.

nodes_gdf.columns

Index(['ns_node_idx', 'x', 'y', 'live', 'weight', 'primal_edge',
       'primal_edge_node_a', 'primal_edge_node_b', 'primal_edge_idx',
       'dual_node', 'cc_beta_500', 'cc_beta_2000', 'cc_cycles_500',
       'cc_cycles_2000', 'cc_density_500', 'cc_density_2000', 'cc_farness_500',
       'cc_farness_2000', 'cc_harmonic_500', 'cc_harmonic_2000',
       'cc_hillier_500', 'cc_hillier_2000', 'cc_betweenness_500',
       'cc_betweenness_2000', 'cc_betweenness_beta_500',
       'cc_betweenness_beta_2000', 'cc_beta_1200', 'cc_cycles_1200',
       'cc_density_1200', 'cc_farness_1200', 'cc_harmonic_1200',
       'cc_hillier_1200', 'cc_betweenness_1200', 'cc_betweenness_beta_1200'],
      dtype='object')

As per the function logging outputs, 15 minutes has been mapped to 1200m at default speed_m_s, so the corresponding outputs can be visualised using the 1200m columns. Use the configurable speed_m_s parameter to set a custom metres per second walking speed.

fig, ax = plt.subplots(1, 1, figsize=(8, 6), facecolor="#1d1d1d")
nodes_gdf.plot(
    column="cc_harmonic_1200",
    cmap="magma",
    legend=False,
    ax=ax,
)
ax.set_xlim(438500, 438500 + 3500)
ax.set_ylim(4472500, 4472500 + 3500)
ax.axis(False)

(np.float64(438500.0),
 np.float64(442000.0),
 np.float64(4472500.0),
 np.float64(4476000.0))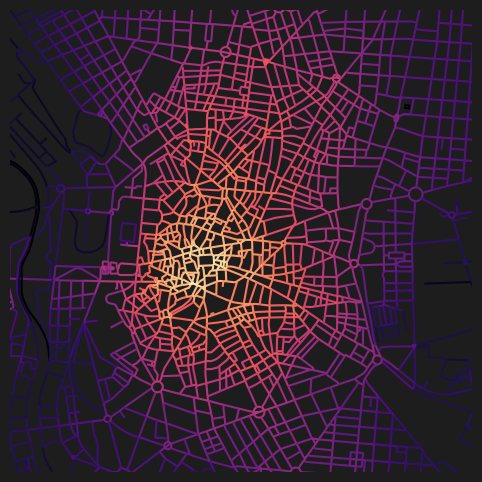

For spatial-impedance weighted forms of centralities (beta variants), you can specify the beta parameter explicitly. These will otherwise be extrapolated automatically from the distances or minutes parameters. See the documentation for more information on how spatial impedances are converted to distance thresholds.

nodes_gdf = networks.node_centrality_shortest(
    network_structure=network_structure,
    nodes_gdf=nodes_gdf,
    betas=[0.01],
)

INFO:cityseer.metrics.networks:Computing shortest path node centrality.
100%|██████████| 47129/47129 [00:01<00:00, 35545.61it/s]
INFO:cityseer.config:Metrics computed for:
INFO:cityseer.config:Distance: 400m, Beta: 0.01, Walking Time: 5.0 minutes.

nodes_gdf.columns

Index(['ns_node_idx', 'x', 'y', 'live', 'weight', 'primal_edge',
       'primal_edge_node_a', 'primal_edge_node_b', 'primal_edge_idx',
       'dual_node', 'cc_beta_500', 'cc_beta_2000', 'cc_cycles_500',
       'cc_cycles_2000', 'cc_density_500', 'cc_density_2000', 'cc_farness_500',
       'cc_farness_2000', 'cc_harmonic_500', 'cc_harmonic_2000',
       'cc_hillier_500', 'cc_hillier_2000', 'cc_betweenness_500',
       'cc_betweenness_2000', 'cc_betweenness_beta_500',
       'cc_betweenness_beta_2000', 'cc_beta_1200', 'cc_cycles_1200',
       'cc_density_1200', 'cc_farness_1200', 'cc_harmonic_1200',
       'cc_hillier_1200', 'cc_betweenness_1200', 'cc_betweenness_beta_1200',
       'cc_beta_400', 'cc_cycles_400', 'cc_density_400', 'cc_farness_400',
       'cc_harmonic_400', 'cc_hillier_400', 'cc_betweenness_400',
       'cc_betweenness_beta_400'],
      dtype='object')

fig, ax = plt.subplots(1, 1, figsize=(8, 6), facecolor="#1d1d1d")
nodes_gdf.plot(
    column="cc_beta_400",
    cmap="magma",
    legend=False,
    ax=ax,
)
ax.set_xlim(438500, 438500 + 3500)
ax.set_ylim(4472500, 4472500 + 3500)
ax.axis(False)

(np.float64(438500.0),
 np.float64(442000.0),
 np.float64(4472500.0),
 np.float64(4476000.0))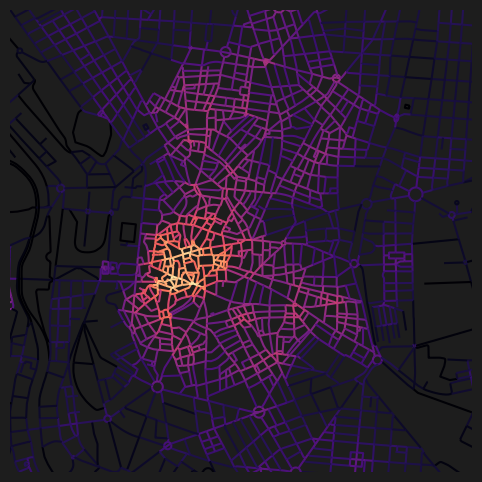

Adaptive centrality for larger distances

For larger distance thresholds, the computational cost increases substantially. The node_centrality_shortest_adaptive function uses an adaptive sampling strategy to compute centralities more efficiently at larger scales while maintaining statistical accuracy.

The target_rho parameter controls the correlation target between the sampled and full computations. A value of 0.95 means the function aims for at least 95% correlation with the exact computation. The function automatically determines which distances require sampling versus full computation, and reports the expected correlation for each distance.

distances = [500, 2000, 5000, 10000]
nodes_gdf = networks.node_centrality_shortest_adaptive(
    network_structure=network_structure,
    nodes_gdf=nodes_gdf,
    distances=distances,
    target_rho=0.95,
)
nodes_gdf.columns

INFO:cityseer.metrics.networks:Computing adaptive shortest path node centrality.
INFO:cityseer.metrics.networks:Probing reachability (50 samples)...
INFO:cityseer.config:
INFO:cityseer.config:Adaptive sampling plan (target ρ ≥ 0.95, internal target 0.97 for both metrics):
INFO:cityseer.config:  Distance │  Reach │ Sample p │ Expected ρ
INFO:cityseer.config:  ─────────┼────────┼──────────┼───────────
INFO:cityseer.config:      500m │     94 │     full │ 1.00 (exact)
INFO:cityseer.config:     2000m │   1099 │     full │ 1.00 (exact)
INFO:cityseer.config:     5000m │   5843 │     27% │ 0.97 (eff_n=1561)
INFO:cityseer.config:    10000m │  20334 │      8% │ 0.97 (eff_n=1561)
INFO:cityseer.metrics.networks:Running per-distance centrality...
INFO:cityseer.metrics.networks:  500m: full...
INFO:cityseer.metrics.networks:  2000m: full...
INFO:cityseer.metrics.networks:  5000m: p=27%...
INFO:cityseer.metrics.networks:    actual: reach=6458, eff_n=1725, expected ρ=0.97
INFO:cityseer.metrics.networks:  10000m: p=8%...
INFO:cityseer.metrics.networks:    actual: reach=21647, eff_n=1662, expected ρ=0.97
INFO:cityseer.metrics.networks:Adaptive centrality complete.

Index(['ns_node_idx', 'x', 'y', 'live', 'weight', 'primal_edge',
       'primal_edge_node_a', 'primal_edge_node_b', 'primal_edge_idx',
       'dual_node', 'cc_beta_500', 'cc_beta_2000', 'cc_cycles_500',
       'cc_cycles_2000', 'cc_density_500', 'cc_density_2000', 'cc_farness_500',
       'cc_farness_2000', 'cc_harmonic_500', 'cc_harmonic_2000',
       'cc_hillier_500', 'cc_hillier_2000', 'cc_betweenness_500',
       'cc_betweenness_2000', 'cc_betweenness_beta_500',
       'cc_betweenness_beta_2000', 'cc_beta_1200', 'cc_cycles_1200',
       'cc_density_1200', 'cc_farness_1200', 'cc_harmonic_1200',
       'cc_hillier_1200', 'cc_betweenness_1200', 'cc_betweenness_beta_1200',
       'cc_beta_400', 'cc_cycles_400', 'cc_density_400', 'cc_farness_400',
       'cc_harmonic_400', 'cc_hillier_400', 'cc_betweenness_400',
       'cc_betweenness_beta_400', 'cc_beta_5000', 'cc_beta_10000',
       'cc_cycles_5000', 'cc_cycles_10000', 'cc_density_5000',
       'cc_density_10000', 'cc_farness_5000', 'cc_farness_10000',
       'cc_harmonic_5000', 'cc_harmonic_10000', 'cc_hillier_5000',
       'cc_hillier_10000', 'cc_betweenness_5000', 'cc_betweenness_10000',
       'cc_betweenness_beta_5000', 'cc_betweenness_beta_10000'],
      dtype='object')

The adaptive function reports the sampling plan during execution, showing which distances use full computation versus sampling. For shorter distances where the number of reachable nodes is small, full computation is used. For larger distances, the function applies sampling to achieve the target correlation efficiently.

fig, ax = plt.subplots(1, 1, figsize=(8, 6), facecolor="#1d1d1d")
nodes_gdf.plot(
    column="cc_betweenness_10000",
    cmap="magma",
    legend=False,
    ax=ax,
)
ax.set_xlim(438500, 438500 + 3500)
ax.set_ylim(4472500, 4472500 + 3500)
ax.axis(False)

(np.float64(438500.0),
 np.float64(442000.0),
 np.float64(4472500.0),
 np.float64(4476000.0))